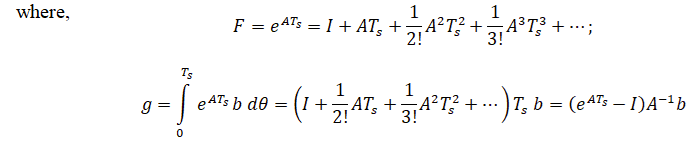Introduction:

Designing digital control systems with a deadbeat response aims to drive the output to the desired value in the shortest time, typically within a finite number of sampling periods, without oscillation or overshoot. This approach is well-suited for applications requiring fast and precise control. Deadbeat control is a linear strategy applied to discrete-time systems, focused on bringing each initial state to zero as quickly as possible.
The controller is designed to reach the target value in exactly N steps, where N corresponds to the number of states in the system. The key idea is to cancel the system's dynamics by placing the poles of the closed-loop system at the origin (or on the unit circle for higher-order systems).
Essentially, the deadbeat controller is the inverse of the plant's transfer function, with adjustments made to ensure stability and practicality. This method guarantees a quick and accurate response while maintaining system integrity.

Deadbeat controller design using State Space model:
Linear time invariant system may be represented in state space form by the following equations:
State equation: $$ \dot{x}(t)=A x(t)+B u(t) \tag{1a} $$ Output equation: $$ y(t)= C x(t) \tag{1b} $$
where, x(t) is state vector, y(t) is output vector, u is input or control vector, A is system matrix, B is input matrix, C is output matrix.

Discrete state space form represented by the following equations:
State equation: $$ {x}[k+1]=F x[k]+g u[k] \tag{2a} $$ Output equation: $$ y[k] = C x[k]\tag{2b} $$

x[k] is state vector, y[k] is output vector, u is input or control vector, F is system matrix, g is input matrix, C is output matrix.

The control input is typically given by:
$$ u[k])= - K x[k] + r[k] \tag{3} $$ where, K is the state feedback gain matrix, r[k] is the reference signal.