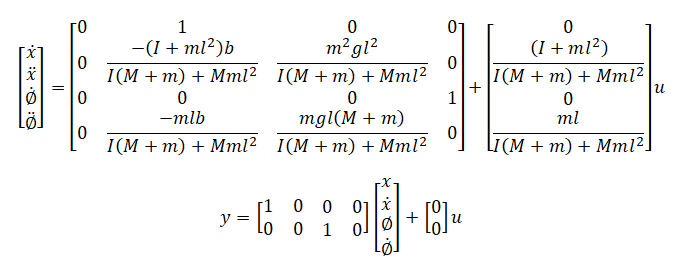Theory:
Linear time invariant system may be represented in state space form by the following equations:
State equation:
$$ \dot{x}(t)=A x(t)+B u(t) \tag{1a} $$
Output equation:
$$ y(t)= C x(t) \tag{1b} $$
State feedback design:
A necessary and sufficient condition for arbitrary pole placement is that the pair (A, B) must be controllable.
Control input:
$$ u(t)= - K x(t) \tag{2} $$
where,
K is the state feedback gain vector,i.e.,
$$ K = [k_1 \ k_2 \ ... \ k_n] $$
With this control input, the closed loop system is as follows:
$$ \dot{x}(t)=(A-BK) x(t) $$
The characteristic equation of the closed loop system is,
$$ |sI-(A-BK)|=0 $$
For
nth order system, the characteristic equation is,
$$ s^n + \alpha_n s^{n-1} + \alpha_{n-1} s^{n-2} + ... + \alpha_1=0 \tag{3} $$
where,
αi for
i=1, 2, ..., n depends on
A, B, K.
The desired closed loop poles are
P1,
P2,
P3, ... ,
Pn.
Then the desired characteristic equation is:
$$ (s-P_1)(s-P_2)(s-P_3)...(s-P_n)=0 \tag{4} $$
The required state feedback gain (
K) vector elements are obtained by comparing the matching coefficients of (3) and (4).
Pre-compensator design:
Control input:
$$ u(t)= - K x(t)+Nr(t) \tag{5} $$
With this control input, the closed loop system is as follows:
$$ \dot{x}(t)=(A-BK) x(t)+ B N r(t) \tag{6} $$
In steady state,
$$ r(t)=r_s, \ x(t)=x_s, \ u(t)=u_s, \ y(t)=y_s, \ \dot{x}(t)=0 \ and \ y_s=r_s \tag{7} $$
From (6) and (7),
$$ 0=(A-BK) x_s+ B N r_s \tag{8} $$
$$ y_s= C x_s \tag{9} $$
From (8),
$$ (A-BK) x_s = - BN r_s $$
$$ x_s = -(A-BK)^{-1}BN r_s \tag{10} $$
From (9) and (10),
$$ y_s = - C (A-BK)^{-1} BN r_s \tag {11}$$
From (7) and (11),
$$ y_s = - C (A-BK)^{-1} BN y_s $$
$$ 1 = - C (A-BK)^{-1} BN $$
$$ N = \frac{-1}{C (A-BK)^{-1} B} \tag{12} $$
where,
N is the pre-compensator gain.
State Space Model of Inverted Pendulumn on cart:
The system consists of an inverted pendulum mounted to a motorized cart. Its popularity derives in part from the fact that it is unstable without control, that is, the pendulum will simply fall over if the cart isn't moved to balance it.
Additionally, the dynamics of the system are nonlinear. The objective of the control system is to balance the inverted pendulum by applying a force to the cart that the pendulum is attached. A real-world example that relates directly to this inverted pendulum system is the attitude control of a booster rocket at takeoff.
In this case we will consider a two dimensional problem where the pendulum is constrained to move in the vertical plane shown in the figure below. For this system, the control input is the force
F that moves the cart horizontally and the outputs are the angular position of the pendulum θ and the horizontal position of the cart
x.
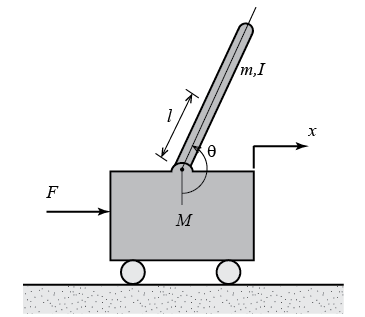 Fig.1. Invereted Pendulum on Cart
Fig.1. Invereted Pendulum on Cart
where,
M is mass of the cart (kg),
m is mass of the pendulum (kg),
b is coefficient of friction for cart (N/m/sec),
l is length to pendulum center of mass (meters),
I is mass moment of inertia of the pendulum (kg.m
2),
F is force applied to the cart,
x is cart position coordinate, θ is pendulum angle from vertical (down).
The linearized equations of motion can also be represented in state space form:
Let Φ represent the deviation of the pedulum's position,
u has been substituted for the input
F.