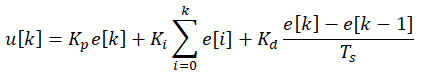Introduction:

Designing a discrete PID controller for a DC motor involves adapting the traditional continuous PID control strategy to a discrete-time system, where the control signal is updated at regular intervals. In real-world applications, especially with digital computers or microcontrollers, the control system operates in discrete time rather than continuous time. A discrete PID controller calculates the control signal at each sampling step based on the error between the desired and actual motor outputs (e.g., speed or position). The discrete PID controller consists of three terms: Proportional (P), Integral (I), and Derivative (D). Each term is computed using the error signal and its past values, with the discrete-time version typically expressed as:

where, e[k] is the error, T_s is the sampling time, K_p, K_i, and K_d are are the controller gains. The design process involves selecting appropriate sampling rates, tuning the PID gains, and ensuring system stability and performance over discrete time steps. The discrete PID controller is essential for digital systems controlling DC motors, offering precise control over motor speed, position, and torque in real-time applications.

Designing a discrete PID controller using State Space Model:
Linear time invariant system may be represented in state space form by the following equations:
State equation: $$ \dot{x}(t)=A x(t)+B u(t) \tag{2a} $$ Output equation: $$ y(t)= C x(t) \tag{2b} $$ Discrete state space form represented by the following equations:
State equation: $$ {x}[k+1]=F x[k]+g u[k] \tag{3a} $$ Output equation: $$ y[k])= C x[k] \tag{3b} $$ Adding Integral State for PID Control:
The integral state is defined as:
$$ x_3 [k+1]=x_3 [k]+T_s(r[k]-x_1 [k]) \tag{4} $$ where, r[k] is the reference input, x₁[k] is the position θ[k].