Theory:
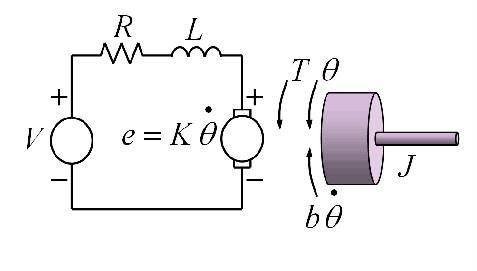Fig.1. DC Motor Model
The DC motor dynamics:
The DC motor dynamics are represted by the following equation:
Mechanical equation:
$$ J\dot{\omega}(t)+K_f {\omega}(t) = K_m i(t) \tag{1}$$
where,
J is the motor inertia,
Kf is the damping coefficient,
Km is the motor constant,
ω(t) is the angular speed of the motor,
i(t) is the armature current,
E b (t) is the back electromotive force, given by
E b (t) =
K b ω(t), and
Kb is the back EMF constant.
Electrical equation:
$$ L \dot{i}(t)+R {i}(t) + E_b (t)= V(t) \tag{2}$$
where,
L is the inductance,
R is the resistance,
i(t) is the armature current,
V(t) is the armature voltage (input).
Transfer Function:
$$ G(s) = \frac{\omega(s)}{V(s)} = \frac{K_m}{JL s^2 + (JR + LK_f) s + (RK_f + K_mK_b)} \tag{3}$$
Pulse Transfer Function:
The bilinear transform is used to transform continuous-time system representation to discrete-time.
$$ s = \frac{1}{T} ln(z) $$
$$ \approx \frac{2}{T} \frac{z -1}{z+1} $$
$$ \approx \frac{2}{T} \frac{1- z^{-1}}{1+z^{-1}}\tag{4} $$
where
Ts is the sampling period.
$$ G(z) = \frac{\omega(z)}{V(z)} = \frac{(z^2+2z+1))K_m}{z^2[\frac{4JL}{{T_s}^2}+\frac{2(LK_f+RJ)}{T_s}+(RK_f+K_mK_b)]+z[2(RK_f+K_mK_b)-\frac{8JL}{{T_s}^2}]+[\frac{4JL}{{T_s}^2}-\frac{2(LK_f+RJ)}{T_s}+(RK_f+K_mK_b)]} \tag{5}$$
$$ G(z) = \frac{\omega(z)}{V(z)} = \frac{(K_m+2K_mz^{-1}+K_m z^{-2})}{[\frac{4JL}{{T_s}^2}+\frac{2(LK_f+RJ)}{T_s}+(RK_f+K_mK_b)]+z^{-1}[2(RK_f+K_mK_b)-\frac{8JL}{{T_s}^2}]+z^{-2}[\frac{4JL}{{T_s}^2}-\frac{2(LK_f+RJ)}{T_s}+(RK_f+K_mK_b)]} \tag{6}$$
State Space Model of the DC motor:
Continuous State Space form:
$$ \begin{bmatrix} \dot{\omega}(t) \\ \dot{i_a}(t) \end{bmatrix} = \begin{bmatrix} -\frac{K_f}{J} & \frac{K_m}{J}\\ -\frac{K_b}{L} & -\frac{R}{L} \end{bmatrix} \begin{bmatrix} \omega(t) \\ i_a(t) \end{bmatrix} + \begin{bmatrix} 0 & \frac{1}{J} \\ \frac{1}{L} & 0\end{bmatrix} \begin{bmatrix} V_a(t) \\ T_d (t) \end{bmatrix} \quad $$
$$ y(t) = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} \omega(t) \\ i_a(t) \end{bmatrix} \quad $$
$$ \tag{7} $$
where,
Td is the load disturbance.
Discrete State Space form:
$$ \begin{bmatrix} \omega [k+1] \\ i_a [k+1] \end{bmatrix} = \begin{bmatrix} 1-\frac{K_f T_s}{J} & \frac{K_m T_s}{J} \\ -\frac{K_b T_s}{L} & 1-\frac{R T_s}{L} \end{bmatrix} \begin{bmatrix} \omega [k] \\ i_a [k] \end{bmatrix} + \begin{bmatrix} \frac{K_m {T_s}^2}{JL} & (\frac{T_s}{J}-\frac{K_f{T_s}^2}{J^2}) \\ (\frac{T_s}{L}-\frac{R{T_s}^2}{L^2}) & -\frac{K_b {T_s}^2}{J^2} \end{bmatrix} \begin{bmatrix} V_a(k) \\ T_d (k) \end{bmatrix} \quad $$
$$ y[k] = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} \omega[k] \\ i_a[k] \end{bmatrix} \quad $$
$$ \tag{8} $$
