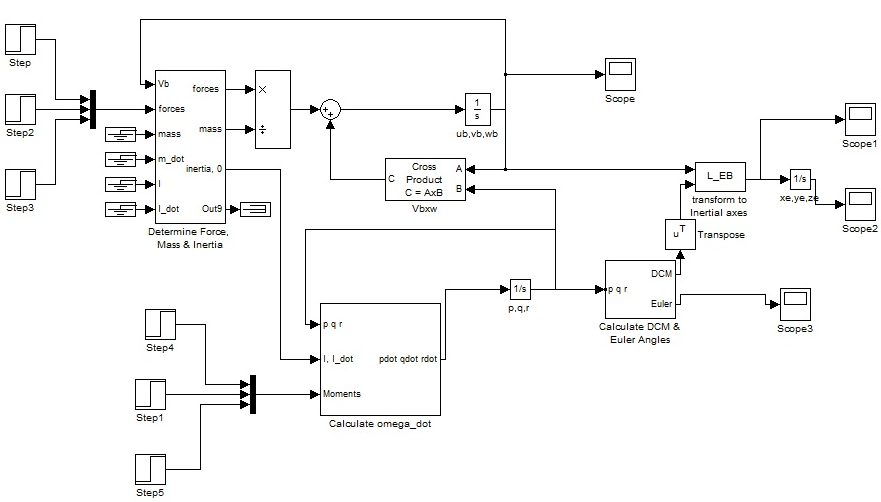
A mathematical modeling and simulation of an autonomous underwater vehicle is done. Mathematical modeling
is done in generalized way, in which six degree of freedom nonlinear model is obtained. With idealized
generic assumptions, the model is simulated using Simulink and response of system is obtained with time. This
study discusses the motion of marine vehicles in 6 degrees of freedom (DOF) since 6 independent coordinates
are necessary to determine the position and orientation of a rigid body. The first three coordinates and their
time derivatives are associated to the position and translation motion along the x, y and z axes,while the
last 3 coordinates and time derivatives are used to describe orientation and rotational motion. For marine
vehicles, the 6 different motion components are conveniently defined as:
surge, sway, heave, roll, pitch and yaw as shown in the table below.
MODELING
Modeling of Marine vehicles involves the study of statics and dynamics. Statics is concerned with the
equilibrium of bodies at rest or moving with constant velocity, whereas dynamics is concerned with bodies
having accelerated motion. It is common to divide the study of dynamics into two parts: kinematics, which
treats only geometrical aspects of motion, and kinetics, which is the analysis of the forces causing the
motion. This study discusses the motion of marine vehicles in 6 degrees of freedom (DOF) since 6
independent coordinates are necessary to determine the position and orientation of a rigid body. The first
three coordinates and their time derivatives are associated to the position and translation motion along
the x, y and z axes,while the last 3 coordinates and time derivatives are used to describe orientation and
rotational motion. For marine vehicles, the 6 different motion components are conveniently defined as:
surge, sway, heave, roll, pitch and yaw as shown in the table below.
 Kinematics
Co-ordinate Frames
Kinematics
Co-ordinate Frames
When analyzing the motion of marine vehicles in 6 DOF it is convenient to define two coordinate frames as
indicated in Figure. The moving coordinate frame XoYoZo is conveniently fixed to the vehicle and is called
the body-fixed reference frame. The origin O of the body-fixed frame is usually chosen to coincide with the
center of gravity(CG) when CG is in the principal plane of symmetry or at any other convenient point if this
is not the case. For marine vehicles, the body axes Xo, Yo and Zo coincide with the principal axes of inertia,
and are usually defined as
Xo = Longitudinal axis (directed from aft to fore)
Yo = Transverse axis (directed to starboard)
Zo = Normal axis(directed from top to bottom)