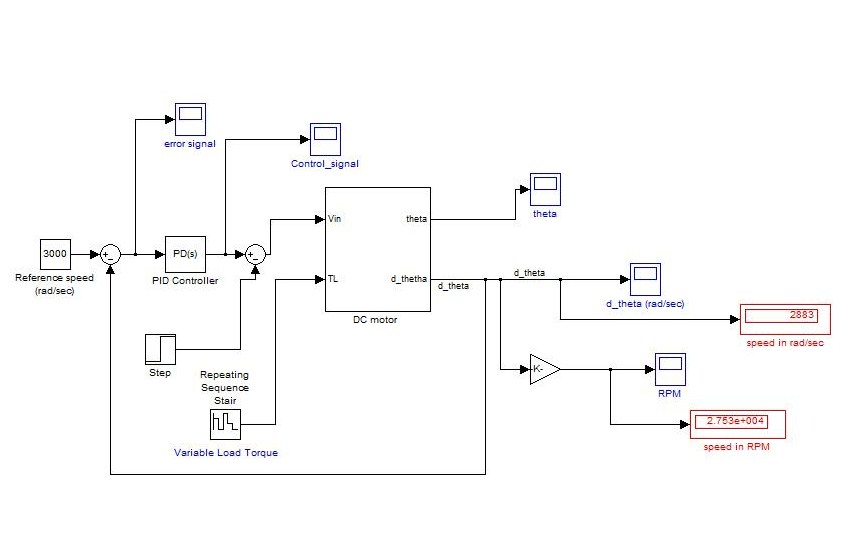
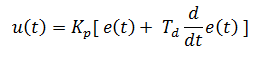CLOSED LOOP CHARACTERISTICS OF DC MOTOR
PROPORTIONAL AND DERIVATIVE CONTROL
Proportional-Derivative control is useful for fast response controllers that do not need a steady-state error of zero.
The effect of proportional and derivative actions is described as below:
Proportional Action
Proportional action provides an instantaneous response to the control error. This is useful for improving the response of a
stable system but cannot control an unstable system by itself. Additionally, the gain is the same for all frequencies leaving
the system with a nonzero steady-state error.
Derivative Action
Derivative action acts on the derivative or rate of change of the control error. This provides a fast response, as opposed to
the integral action, but cannot accommodate constant errors (i.e. the derivative of a constant, nonzero error is 0). Derivatives
have a phase of +90 degrees leading to an anticipatory or predictive response. However, derivative control will produce large
control signals in response to high frequency control errors such as set point changes (step command) and measurement noise.
Proportional-Derivative (PD) Control
Proportional-Derivative or PD control combines proportional control and derivative control in parallel.
It can be mathematically expressed as:
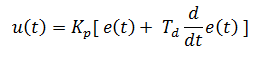
where
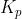
is the Proportional control gain and
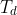
is the derivative time.
Design Considerations
With proportional controller alone the shape of the open loop transfer function will be the same as the plant but the
overall magnitude of the plant will be higher. With derivative control the open loop transfer function above the frequency of
the derivative (zero) will have a +20 dB/decade slope. The phase will gain +90 deg above the zero as well.
Proportional control will follow the noise and amplify it by the magnitude of the controller. Derivative control will
amplify noise by following the difference between two noisy error signals. One should keep these things in mind while designing
a PD control.