

Virtual Lab on Robotics and Control
Sponsored by Ministry of Human Resource and Development, INDIA.Indian Institute of Technology Kharagpur


Sponsored by Ministry of Human Resource and Development, INDIA.Indian Institute of Technology Kharagpur
The aim of the experiment is to understand a typical 6-arm robot manipulator. Here we demonstrate the robot PUMA 560.
General Terminology in Robotics:
Workspace:
The reachable workspace of a robot's end-effector is the manifold of reachable frames.
Accuracy:
Accuracy refers to a robot's ability to position its wrist end at a desired target point within the work volume, and it is defined in terms of spatial resolution. It depends on the technology and the control increments.
Repeatability:
Repeatability is a statistical term associated with accuracy. If a robot joint moves by the same angle from a certain point a number of times, all with equal environmental conditions, the target is always missed by a large margin. If the same error is repeated, then we say that the repeatability is high and the accuracy is poor.
Safety:
The ability to reduce the human-robot impact force and ensure human safety is a fundamental requirement for human-friendly robots.
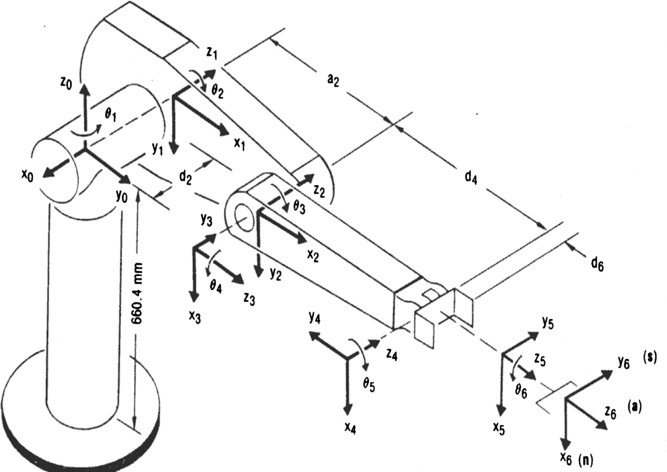
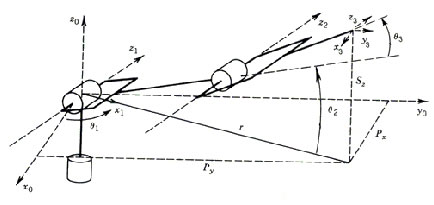
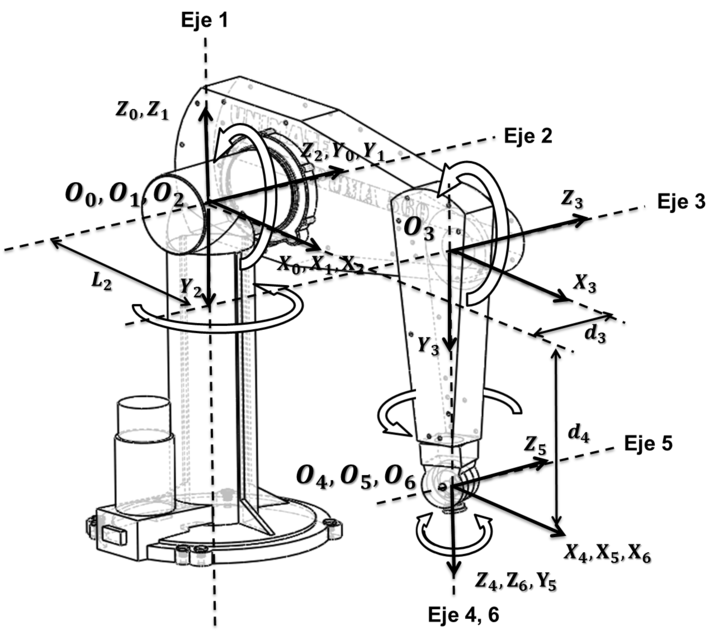
Forward Kinematics :
Forward kinematics (FK) mainly deals with constructing a Denavit-Hartenberg (D-H) transformation matrix with Puma's parameters obtained from a D-H parameter table shown below:
Table 1. Puma 560 D-H parameter table
| Link | a(m) | (deg) | d(m) | (deg) |
| 1 | 0 | 90 | 0.67 | * |
| 2 | 0.4318 | 0 | 0 | * |
| 3 | 0.4318 | -90 | 0.15005 | * |
| 4 | 0 | 90 | 0 | * |
| 5 | 0 | -90 | 0 | * |
| 6 | 0 | 0 | 0 | * |
Transformation matrices of six joints:
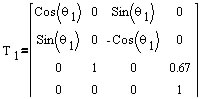 |
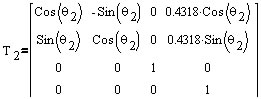 |
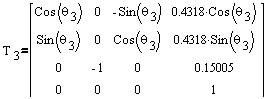 |
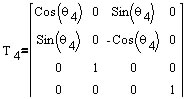 |
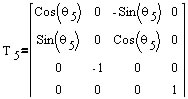 |
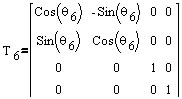 |
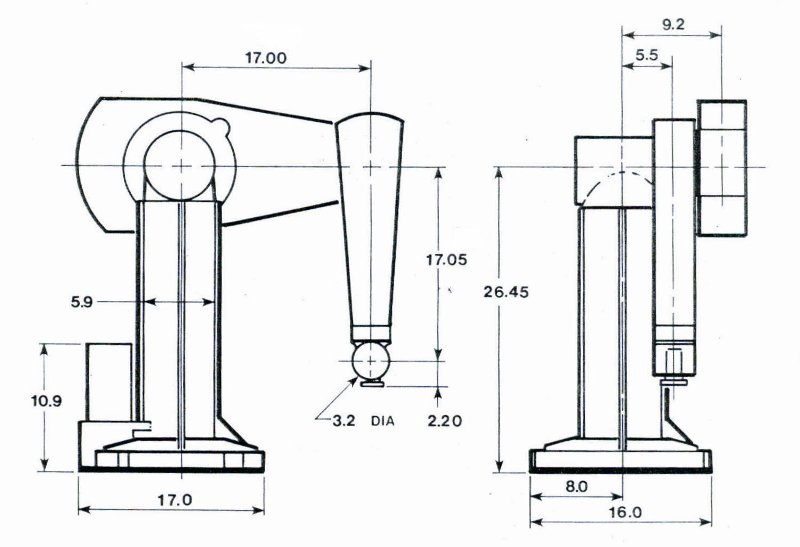
Puma kinematic diagrams:
 |
|
 |
|
This program simulates a 7 link 3D Puma Robot using the cad2matdemo program. The software derives the data, to develop simulation of PUMA 560, from the CAD file imported to Matlab using cad2matdemo.m. The software then uses this data to produce the simulation of the motion specified by user.
The software interacts with the user through a GUI, where it takes input from the user in terms of the angular motion of different arms, and shows the output in the form of a simulation. The angular displacement can be provided by either a slider with a discrete variation or directly a numerical value can be provided in a text box.The software does not allow for the specification of angular speed or acceleration of the arms. These values are fixed in the code.
Kinematics Panel consists of
| Angle | Range | Default | Angle |
| Theta 1:320 | -160 to 160 | 90 | Waist Joint |
| Theta 2:220 | -110 to 110 | -90 | Shoulder Joint |
| Theta 3:270 | -135 to 135 | -90 | Elbow Joint |
| Theta 4:532 | -266 to 266 | 0 | Wrist Roll |
| Theta 5:200 | -100 to 100 | 0 | Wrist Bend |
| Theta 6:532 | -266 to 266 | 0 | Wrist Swivel |
Besides these, the GUI has the following buttons:
Random: A random input is provided and the robot animates between locations.
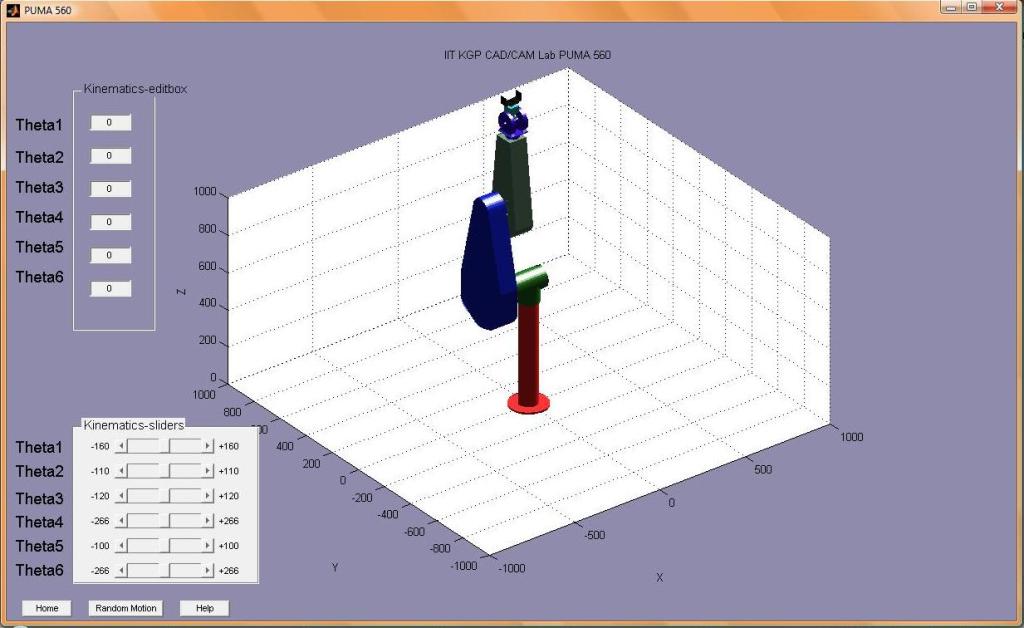
The page shows the figure after simulation and updates the image with the last figure
The page shows the animation through a series of figures by incrementally increasing the angle using Java Session